Answer:
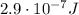
Step-by-step explanation:
The energy density associated to a magnetic field is:
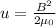 (1)
(1)
where
B is the strength of the magnetic field
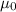 is the vacuum permeability
is the vacuum permeability
The magnetic field produced by a current-carrying wire is
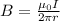
where
I is the current in the wire
r is the distance from the wire at which the field is calculated
Substituting into (1),
 (2)
(2)
Since this is the energy density, the total energy stored in a certain element of volume
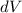 will be
will be
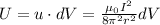 (3)
(3)
Here the field strength changes as we move farther from the wire radially, so we can write dV as

where
h is the height of the cylinder
r is the distance from the wire
So eq(3) becomes:
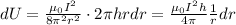
Now we have to integrate this expression to find the total energy stored in the cylindrical volume. We have:
h = 50 mm = 0.050 m is the height of the cylinder
I = 4.9 A is the current in the wire
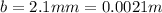 is the internal radius of the cylinder (the radius of the wire)
is the internal radius of the cylinder (the radius of the wire)
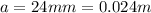 is the external radius of the cylinder
is the external radius of the cylinder
So,
![U=\int\limits^a_b {dU} =(\mu_0 I^2 h)/(4\pi) \int\limits^(0.024)_(0.0021) (1)/(r)dr = (\mu_0 I^2 h)/(4\pi) [ln(a)-ln(b)]=\\=((4\pi \cdot 10^(-7))(4.9)^2(0.050))/(4\pi)[ln(0.024)-ln(0.0021)]=2.9\cdot 10^(-7) J](https://img.qammunity.org/2021/formulas/physics/high-school/7jm2ose2qcovk5powt2r2pyestdyh5cax9.png)