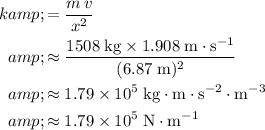Answer:
Approximately
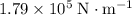 , assuming friction between the vehicle and the ground is negligible.
, assuming friction between the vehicle and the ground is negligible.
Step-by-step explanation:
Let
 denote the mass of the vehicle. Let
denote the mass of the vehicle. Let
 denote the initial velocity of the vehicle. Let
denote the initial velocity of the vehicle. Let
 denote the spring constant (needs to be found.) Let
denote the spring constant (needs to be found.) Let
 denote the maximum displacement of the spring.
denote the maximum displacement of the spring.
Convert velocity of the vehicle to standard units (meters per second):
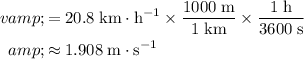 .
.
Initial kinetic energy (
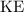 ) of the vehicle:
) of the vehicle:
 .
.
When the vehicle is brought to a rest, the elastic potential energy (
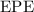 ) stored in the spring would be:
) stored in the spring would be:
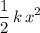 .
.
By the conservation of energy, if the friction between the vehicle and the ground is negligible, the initial
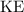 of the vehicle should be equal to the
of the vehicle should be equal to the
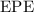 of the vehicle. In other words:
of the vehicle. In other words:
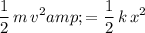 .
.
Rearrange this equation to find an expression for
 , the spring constant:
, the spring constant:
 .
.
Substitute in the given values
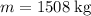 ,
,
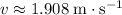 , and
, and
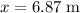 :
: