Answer:
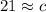
Step-by-step explanation:
Solving for Angles
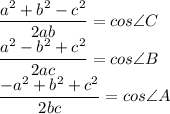
Do not forget to use
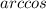 or
or
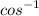 towards the end, or the result will be thrown off.
towards the end, or the result will be thrown off.
Solving for Edges
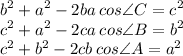
Take the square root of the result in the end, or you will throw yourself off.
Well, let us get to work:
![\displaystyle 13^2 + 29^2 - 2[13][29]cos\:41 = c^2 \\ 169 + 841 - 754cos\:41 = c^2 \\ 1010 - 754cos\:41 = c^2 \\ \\ √(440,94897651...) = √(c^2) \\ 20,99878512... = c \\ \\ \boxed{21 \approx c}](https://img.qammunity.org/2023/formulas/mathematics/college/5vcuqykhiknrmqx7byqt2uqz3083ffl4i8.png)
I am joyous to assist you at any time.