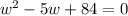Question

The length of a rectangle is five less than its width. The area of the rectangle is 84 square feet. Write a quadratic equation in standard form, ax^2+bx+c=0

Answer 1

Given:

The length of a rectangle is 5 less than its width.

The area of the rectangle is 84 square feet.

We need to determine the quadratic equation in standard form that represents the area of the rectangle.

Dimensions of the rectangle:

Let l denote the length of the rectangle.

Let w denote the width of the rectangle.

Since, it is given that the length is 5 less than its width, it can be written as,

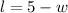`l=5-w` and
`w=w`

Area of the rectangle:

The area of the rectangle can be determined using the formula,

`A=length * width`

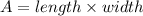
Substituting A = 84,
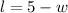`l=5-w` and
`w=w`, we get

`84=(5-w)* w`

`84=5w-w^2`

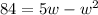
Adding both sides of the equation by w², we have;

`w^2+84=5w`

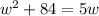
Subtracting by 5w on both sides, we get;

`w^2-5w+84=0`

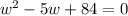
Thus, the quadratic equation in standard form for the area of the rectangle is
`w^2-5w+84=0`