Given:
The length of a rectangle is 6 meters more than its width.
The area of the rectangle is 135 square feet.
We need to determine the quadratic equation in standard form that represents the area of the rectangle.
Dimensions of the rectangle:
Let l denote the length of the rectangle.
Let w denote the width of the rectangle.
Since, it is given that the length is 6 more than its width, it can be written as,
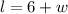 and
and

Area of the rectangle:
The area of the rectangle can be determined using the formula,
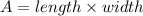
Substituting A = 135,
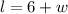 and
and
 , we get
, we get
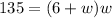

Subtracting both sides by 135, we get;
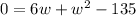
Switch sides, we get;

Thus, the quadratic equation in standard form for the area of the rectangle is
