Answer:
Which expression is equal to
![\sqrt[3]{64}a^6b^7c^9](https://img.qammunity.org/2021/formulas/mathematics/middle-school/egc6polqvs3fwfywbilalejpt0q3er069h.png) ?
?
The correct answer is B.
![4a^(2)b^(2)c^(3)(\sqrt[3]{b})](https://img.qammunity.org/2021/formulas/mathematics/middle-school/mq1c2ac3nui2o2qwh3vrbapss1wtzyjvw5.png)
Explanation:
Inside of the radical you have
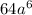 . If you find the cube root of that, you get 4a^2. Go ahead and write that outside of the parenthesis:
. If you find the cube root of that, you get 4a^2. Go ahead and write that outside of the parenthesis:
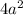

c^(9)})](https://img.qammunity.org/2021/formulas/mathematics/middle-school/qjh0yj5hev0d9qzsmu7u2rdyi33nx62quu.png)
If you re-write what is inside of the radical, you get:
![4a^(2)(\sqrt[3]{b^(3)*b^(3)*b^(1)*c^(3)*c^(3)*c^(3) }](https://img.qammunity.org/2021/formulas/mathematics/middle-school/73p9no254s6czhcinut6kjmblqezgfwu0b.png)
Basically I expanded what was inside of the radical so I could find the cube roots of b^7 and c^9.
Now, take the cube root of b^7:
![4a^(2)b^(2) (\sqrt[3]b*c^(3)*c^(3)*c^(3) })](https://img.qammunity.org/2021/formulas/mathematics/middle-school/3dgqwgqclgmk9z485k1ekxcr4tuvc288mv.png)
Notice how I could only factor out the two "b^3" that were inside the radical symbol, and how I left the b^1 inside the radical symbol because I couldn't factor it out.
Let's now get the cube root of c^9. Since it's a perfect cube, there won't be any "c"s left inside of the radical symbol:
![4a^(2)b^(2)c^(9)(\sqrt[3]b)](https://img.qammunity.org/2021/formulas/mathematics/middle-school/xtnkmw1mewl2cio2p2nnuud252vzn8sc98.png)