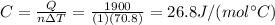Answer:
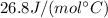
Step-by-step explanation:
The molar mass of water is
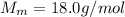
Here the mass of water is
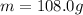
So the number of moles of water in the cup is:

The amount of heat released by absorbed by the water in the process is:
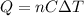
where
n = 6 mol is the number of moles
C = 75.4 J / (mol•°C) is the molar heat capacity of water
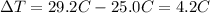 is the change in temperature of the water
is the change in temperature of the water
Substituting,
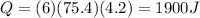
According to the law of conservation of energy, this is also equal to the energy released by the hot tin metal, which can be rewritten as
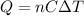
where:
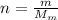 is the number of moles of tin, where
is the number of moles of tin, where
m = 118.7 g is the mass of tin
 is the molar mass of tin
is the molar mass of tin
So,

C is the molar heat capacity of tin
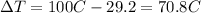 is the change in temperature of the tin
is the change in temperature of the tin
Solving for C, we find the molar heat capacity of tin: