Question

8.5 Exercises

In Exercises 1-20 use the Laplace transform to solve the initial value problem. Where indicated by C/G, graph the solution.

#17.

y" + 3y' + 2y = {

e⁻ᵗ, 0 ≤ t < 1

0, t ≥ 1

y(0) = 1

y'(0) = - 1​

Answer 1

We can express the forcing function (the piecewise expression on the right side) in terms of the step function as
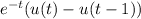`e^(-t)(u(t) - u(t-1))` where

`u(t) = \begin{cases}1&\text{for }t\ge0\\0&\text{otherwise}\end{cases}`

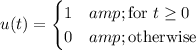
Let F(s) be the Laplace transform of a function f(t). Now recall the transform pair

`f(t-c) u(t-c) \mapsto e^(-cs) F(s)`

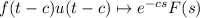
This means

`e^(-t) u(t) \mapsto \frac1{s+1}`

`e^(-t) u(t-1) = \frac1e * e^(-(t-1)) u(t-1) \mapsto  (e^(-(s+1)))/(s+1)`

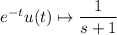
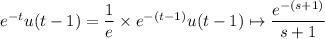
I assume you're familiar with the transform rule for derivatives of y(t). Now we're ready to take the transform of both sides of the ODE:

`y'' + 3y' + 2y = e^(-t)(u(t) - u(t-1))`

`\implies \left(s^2 Y(s) - s y(0) - y'(0)\right) + 3 \left(s Y(s) - y(0)\right) + 2 Y(s) = (1 - e^(-(s+1)))/(s+1)`

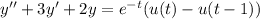
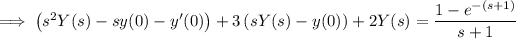
Plug in the initial values and solve for Y(s) :

`\left(s^2 Y(s) - s + 1\right) + 3 \left(s Y(s) + 1\right) + 2 Y(s) = (1 - e^(-(s+1)))/(s+1)`

`(s^2 + 3s + 2) Y(s) - s + 4 = (1 - e^(-(s+1)))/(s+1)`

`Y(s) = (1 - e^(-(s+1)) + (s-4)(s+1))/((s+1)(s^2 + 3s + 2))`

`Y(s) = (1 - e^(-(s+1)) + (s-4)(s+1))/((s+1)^2 (s+2))`

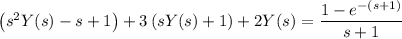
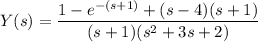
Consider the partial fraction expansion

`\frac1{(s+1)^2(s+2)} = \frac a{s+1} + \frac b{(s+1)^2} + \frac c{s+2}`

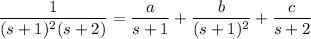
Solve for the coefficients:

`1 = a(s+1)(s+2) + b(s+2) + c(s+1)^2`

`s = -1 \implies b = 1`

`s = -2 \implies c = 1`

`1 = (a+c)s^2 + \cdots \implies a+c = 0 \implies a = -1`

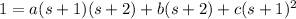
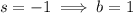
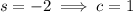
Hence we can expand Y(s) as

`Y(s) = \frac1{(s+1)^2} + \frac1{s+2}  + (e^(-(s+1)))/(s+1) - (e^(-(s+1)))/((s+1)^2) - (e * e^(-(s+2)))/(s+2)`

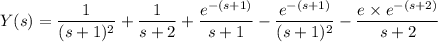
The last transform pair we need is

`e^(ct) f(t) \mapsto F(s - c)`

Now, taking inverse transforms of everything yields

`\frac1{(s+1)^2} \mapsto te^(-t)`

`\frac1{s+2} \mapsto e^(-2t)`

`(e^(-(s+1)))/(s+1) \mapsto e^(-t) u(t-1)`

`(e^(-(s+1)))/((s+1)^2) \mapsto e^(-t) (t-1) u(t-1)`

`(e * e^(-(s+2)))/(s+2) \mapsto e^(-(2t-1)) u(t-1)`

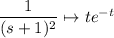
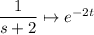
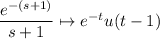
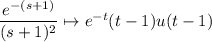
and putting everything together gives the same solution as the one provided.