Answer:
The angular momentum is same as it was before.
The rotation period is
 times the original period.
times the original period.
The rotational kinetic energy is 9452 times greater.
Step-by-step explanation:
The angular momentum
 of a rigid body is
of a rigid body is
 ,
,
where
 is the moment of inertia and
is the moment of inertia and
 is the angular velocity.
is the angular velocity.
Now, the law of conservation of momentum demands that
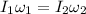 ,
,
in words this means the angular momentum before must equal the angular momentum after.
Let us call
 the mass,
the mass,
 the radius, and
the radius, and
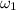 the angular velocity of the sun before it becomes a white dwarf, then its linear momentum is
the angular velocity of the sun before it becomes a white dwarf, then its linear momentum is
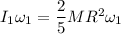 (Remember for a solid sphere
(Remember for a solid sphere
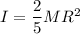 )
)
After it has become a white dwarf, the suns mass is 80% of what it had before (went off by 20%), and its radius has become 0.0115% its initial value (8000 km is 0.0115% of the radius of the sun ); therefore, the angular momentum is
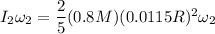
which must be equal to the angular momentum it had before; therefore
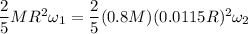
which we solve for
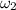 :
:
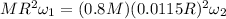
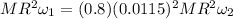
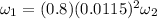
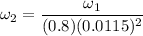
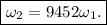
which is about whopping 9500 times larger than initial angular velocity!!
Now the rotation period
 is
is


since
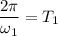
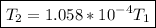
Similarly, the rotation kinetic energy will be
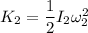
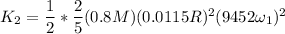
![K_2 =0.8*0.0115^2*9452^2 [(1)/(2)*(2)/(5) mR^2w_1^2]](https://img.qammunity.org/2021/formulas/physics/college/a2d9rhm50vugba4hroafvh2g8be592a4fw.png)
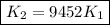
which is about 9500 times larger than initial rotational kinetic energy!