Question

A stop sign is a regular octagon. The standard stop sign has a 16.2 inch radius. The area of a standard stop sign is _______________

square inches. Please round your answer to the nearest whole number

Answer 1

The area of standard stop sign regular octagon is 742.3 squared inches, if the standard stop sign has a 16.2 inch radius.

Explanation:

The given is,

Radius of standard stop sign is 16.2 inch radius

Step:1

The regular octagon is equal to the 16 right angled triangle,

Angle of right angle triangle =
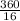`(360)/(16)` = 22.5°

Ref attachment,

From the OAB right angle triangle,

Trigonometric ratio,

sin ∅ =
`(Opp)/(Hyp)`

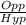
Where, ∅ = 22.5°

Hyp = Radius = 16.2 inches

Ratio becomes,

sin 22.5°=
`(b)/(16.2)`

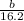
b = (0.374607)(16.2)

b = 6.19947 inches

Trigonometric ratio,

cos ∅ =
`(Adj)/(Hyp)`

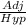
Where, ∅ = 22.5°

Hyp = Radius = 16.2 inches

Adj = h

Ratio becomes,

cos 22.5°=
`(h)/(16.2)`

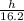
h = (0.9238795)(16.2)

h = 14.967 inches

Step:2

From the triangle OAC,

Area,
`A = (1)/(2) (Height )( Base)`

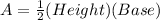
Where, Height = 14.967 inches

Base = b + x = 6.19947 + 6.19947

= 12.3989 inches

From the values equation becomes,

A =
`(1)/(2) (14.967)(12.39894)`

A = 92.7875 Squared inches

Step:3

The octagon is equal to sum of 8 triangles

Area of octagon = 8 × Area of triangle

= 8 × 92.7875

= 742.3 squared inches

Result:

The area of standard stop sign regular octagon is 742.3 squared inches, if the standard stop sign has a 16.2 inch radius.