1) 10.8 cm, shrunken
2) 19.7 cm
3) 8.8 cm
4) See explanation
Step-by-step explanation:
1)
A mirror works on the principle of reflection: a ray of light coming from an object is reflected back by the mirror, producing an image of the object.
The position of the image can be found by using the mirror equation:
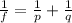
where
f is the focal length of the mirror
p is the position of the object
q is the location of the image
In this problem:
f = 7 cm is the focal length of the mirror
p = 20 cm is the position of the object
So we can find q from the equation:
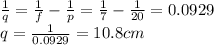
The sign of q is positive: this means the image is real.
The magnification of the image is given by
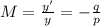
where
y' is the size of the image
y is the size of the object
M is the magnification
Substituting,
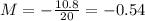
Which means that he image is shrunken, (because
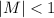 ), so
), so
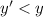 .
.
2)
A lens works on the principle of refraction: the rays of light coming from an object are refracted into the focal point of the lens, and they can produce an image of the object.
We can solve the problem by using the lens equation:
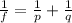
where
f is the focal length of the length
p is the position of the object
q is the location of the image
In this problem we have:
q = 51.5 cm is the location of the image
p = 32 cm is the position of the object
Solving for f, we find the focal length:
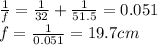
3)
In this problem, we know the following data:
 is the focal length (for a converging lens, it is positive)
is the focal length (for a converging lens, it is positive)
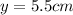 is the height of the object
is the height of the object
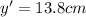 is the height of the image
is the height of the image
 is the location of the image (it is negative because the image is virtual)
is the location of the image (it is negative because the image is virtual)
From the magnification equation, we can find the position of the object:
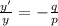
And solving for p, the position of the object, we find:
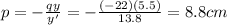
So, the object should be located 8.8 cm from the lens.
4)
The images produced by a lens or by a mirror can be of two types:
- Real: a real image is produced when the refracted (or reflected) rays actually meet behind the lens (or in front of the mirror). In this case, the image can be actually projected on a screen. A real image is located behind the lens (or in front of the mirror).
- Virtual: a virtual image is produced when the refracted (or reflected) rays do not meet at any point, so no image can be actually projected on a screen. In this case, the image forms from the intersection of the prolongation of the refracted/reflected rays. A virtual image is located in front of the lens (or behind the mirror).