Question

Which best describes the relationship among the volumes of hemisphere X, cylinder Y, and cone Z?

A. The sum of the volumes of X and Y equals the volume of Z.

B. The sum of the volume of X and Z equals the volume of Y.

C. The difference of the volumes of Z and Y equals the volume of X.

D. The difference of the volumes of X and Z equals the volume of Y.

Answer 1

B. The sum of the volume of X and Z equals the volume of Y.

Explanation:

To solve the problem, we calculate the volume of the three solids, and then we compare them.

The volume of X is the volume of a hemisphere of radius r, which is half the volume of a sphere of radius r, so:

`V_x = (1)/(2)((4)/(3)\pi r^3)=(2)/(3)\pi r^3`

The volume of Y is the volume of a cylinder of radius r and height

h = r

so it is given by the formula:

`V_Y=\pi r^2 h = \pi r^2 \cdot r = \pi r^3`

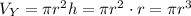
Finally, the volume of Z is the volume of a cone of radius r and height

h = r

So the volume is given by

`V_Z = (1)/(3)\pi r^2 h = (1)/(3)\pi r^2 \cdot r = (1)/(3)\pi r^3`

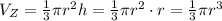
So we see that the correct option is

B. The sum of the volume of X and Z equals the volume of Y.

In fact:

`V_X + V_Z = (2)/(3)\pi r^3 + (1)/(3)\pi r^3 = \pi r^3 = V_Y`