ΔNJH and ΔΝQΡ are the best pair of triangles to prove similarity, based on the SAS similarity criterion and the resulting correlation between their slopes. Thus, the correct option is A.
The best pair of triangles that can be shown similar to complete the proof is ΔNJH and ΔΝQΡ.
To prove this, we can use the SAS similarity criterion, which states that two triangles are similar if two of their corresponding sides are proportional and the angle included by these sides is congruent. In this case, corresponding sides AN and QR are proportional, as are corresponding sides JH and QP. Additionally, the angle included by these sides, ∠ANJ = ∠QRP, is congruent by vertical angles. Therefore, we can conclude that ΔNJH ~ ΔΝQΡ.
This similarity relationship can then be used to demonstrate that the slopes of the two perpendicular lines are opposite reciprocals. Since ΔNJH and ΔΝQΡ are similar, we can set up the following proportion:

Isolating AN in the first equation, we get:

Substituting this expression for AN into the second equation, we obtain:
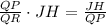
Simplifying the right side of this equation, we have:
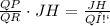
Canceling the JH terms on both sides, we arrive at:
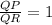
This implies that the slopes of the two perpendicular lines, m∠A and m∠N, are opposite reciprocals. Therefore, the given statement is true, and ΔNJH ~ ΔΝQΡ is the pair of triangles that can be proved similar to complete the proof.
So, the correct option is A: ΔNJH ~ ΔΝQΡ