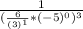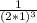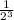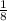Question

Which is the value of this expression when m equals 3 and n equals -5

(6m with exponent of -1 x n with the exponent of 0) another exponent of -3

Answer 1

When you have a negative exponent, you move the base with the negative exponent to the other side of the fraction to make the exponent positive.

For example:

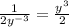`(1)/(2y^(-3)) =(y^3)/(2)` ("y" is the base with the negative exponent)

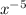`x^(-5)` or
`(x^(-5))/(1) =(1)/(x^5)`

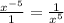
When you multiply an exponent directly to a base with an exponent, you multiply the exponents together.

For example:

`(y^3)^2=y^((3*2))=y^6`

`(x^2)^4=x^((2*4))=x^8`

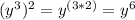
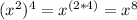
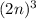`(2n)^3` or
`(2^1n^1)^3=2^((1*3))n^((1*3))=2^3n^3=8n^3`

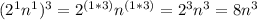
When you have an exponent of 0, the result will always equal 1

For example:

`x^0=1`

`5^0=1`

`y^0=1`

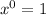
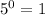
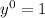
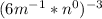`(6m^(-1)*n^0)^(-3)` I think you should first make the exponents positive

`(1)/(((6)/(m^1) *n^0)^3)`

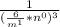
Since you know:

m = 3

n = -5 Substitute/plug it into the equation

`(1)/(((6)/((3)^1)*(-5)^0)^3 )`

`(1)/((2*1)^3)`

`(1)/(2^3)`

`(1)/(8)`