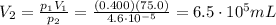Question

3. A sample of krypton gas occupies 75.0 mL at 0.400 atm. If the temperature remained constant, what volume would the krypton occupy at:

c. 765 mmHg; d. 4.00 mmHg; e. 3.50x10-2

Answer 1

c) 29.8 mL

d) 5375 mL

e)
`6.5\cdot 10^5 mL`

Step-by-step explanation:

c)

We can solve this problem by using Boyle's Law, which states that:

"For a fixed mass of an ideal gas kept at constant temperature, the pressure of the gas is inversely proportional to its volume"

Mathematically:

`pV=const.`

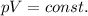
where

p is the pressure of the gas

V is its volume

We can rewrite the formula as

`p_1 V_1 = p_2 V_2`

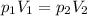
For the gas in this problem:

`p_1=0.400 atm` is the initial pressure

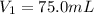`V_1=75.0 mL` is the initial volume

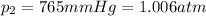`p_2=765 mmHg = 1.006 atm` is the final pressure (using the conversion factor
`1 atm = 760 atm`)

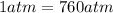Solving for V2, we find the final volume:

`V_2=(p_1 V_1)/(p_2)=((0.400)(75.0))/(1.006)=29.8 mL`

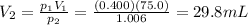
d)

We can solve this part by using again the equation:

`p_1 V_1 = p_2 V_2`

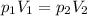
Where in this case we have:

`p_1=0.400 atm` is the initial pressure

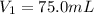`V_1=75.0 mL` is the initial volume

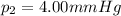`p_2=4.00 mmHg` is the final pressure

Converting into atmospheres,

`p_2 = 4.00 mmHg \cdot (1)/(760 mmHg/atm)=0.0053 atm`

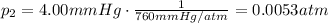
And solving for V2, we find the final volume:

`V_2=(p_1 V_1)/(p_2)=((0.400)(75.0))/(0.0056)=5357 mL`

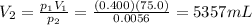
e)

As before, we use Boyles' Law:

`p_1 V_1 = p_2 V_2`

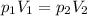
In this part we have:

`p_1=0.400 atm` is the initial pressure of the gas

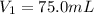`V_1=75.0 mL` is the initial volume of the gas

`p_2=3.50\cdot 10^(-2) torr`

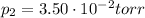
1 torr is equivalent to 1 mmHg, so the conversion factor is the same as before, therefore the final pressure in atmospheres is:

`p_2 = 3.50\cdot 10^(-2) mmHg \cdot (1)/(760 mmHg/atm)=4.6\cdot 10^(-5) atm`

And so, the final volume of the krypton gas is:

`V_2=(p_1 V_1)/(p_2)=((0.400)(75.0))/(4.6\cdot 10^(-5))=6.5\cdot 10^5 mL`