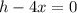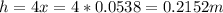Question

You have a spring hanging vertically. You add a mass to the end and let it stretch to find its new equilibrium position which is 5.38 cm below the unstretched position.

You now raise the mass (compress the mass-spring system) to a position that is 5.38 above its original unstretched position. Now you release the mass.

How far from this starting position does it travel downward until it stops and changes direction?

Answer 1

The mass attached to the spring in simple harmonic motion will move downward from its starting position by 5.38 cm before it comes to a stop and reverses direction.

Step-by-step explanation:

When you compress a mass-spring system above its natural length and release it, the system will undergo simple harmonic motion (SHM). In the case described, you have compressed the spring to a position 5.38 cm above the unstretched position and then released it. The system will oscillate around the equilibrium position, and the mass will travel downward until it reaches an amplitude of motion that matches the compression distance. Therefore, the mass will move downward from its starting position by 5.38 cm before it stops and changes direction.

Answer 2

0.2152 m

Step-by-step explanation:

5.38 cm = 0.0538 m

Let m be the mass of the spring, g = 9.81 m/s2 be the gravitational constant. Then the spring constant can be calculated if it's stretched x = 0.0538m under the gravity by such mass

kx = mg

k = (mg)/x (1)

Let h be the total vertical distance traveled from the starting position to the bottom when it changes direction. When the spring is at the position that is 0.0538 above its original unstretched position, it is compressed by a length of x = 0.0538. When it reaches the bottom, then it is stretched by a length of h - x. Using the equation of energy conservation, we have:

`kx^2/2 + mgh = k(h-x)^2/2`

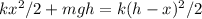
From here we can solve for h in term of other variables:

`kx^2 + 2mgh = k(h-x)^2`

`x^2 + 2mgh/k = (h-x)^2`

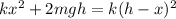
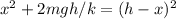
We can substitute k = (mg)/x:

`x^2 + 2hx = h^2 - 2hx + x^2`

`h^2 - 4hx = 0`

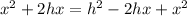
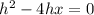
As h can't be 0, we can divide both sides by h

`h - 4x = 0`

`h = 4x = 4*0.0538 = 0.2152 m`