Question

A square coil ℓ = 2cm on a side with 30 turns rotates in a uniform magnetic field, B~ = B0zˆ = 0.1Tˆz, such that the normal of the coil is aligned with the field once per rotation. The coil rotates once every T = 5s and starts with its normal parallel to the field. (a)Write the magnetic flux as a function of time symbolically. Report the numeric values for any constants you introduce separately. (b)Compute the induced emf at t = 12.5s. Report both a symbolic and numeric value.

Answer 1

a) 1.2*10^{-3}cos(1.25t)

b) 0.49mV

Step-by-step explanation:

a) The coil rotates periodically with period T. Hence, we can write the variation of the magnetic flux with a sinusoidal function, and with max flux NAB. Thus, we have that:

`\Phi_B(t)=NABcos(\omega t)\\\\\omega=(2\pi)/(T)=1.25(rad)/(s)\\\\A=l^2=(0.02m)^2=4*10^(-4)m^2\\\\B=0.1T\\\\\Phi_B(t)=1.2*10^(-3)cos(1.25 t) W`

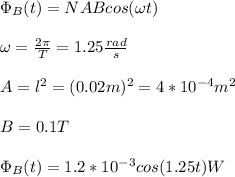
where we have used the values given by the information of the problem for N B and A.

b)

the emf is given by:

`emf=-(d\Phi_B)/(dt)=-NBA\omega sin(\omega t)\\\\emf(t=12.5s)=-(30)(0.1T)(4*10^(-4))(1.25(rad)/(s))sin(1.25*12.5)=1.49*10^(-4)V=0.49mV`

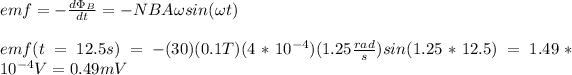
hope this helps!!