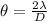Question

If the opening to the harbor acts just like a single-slit which diffracts the ocean waves entering it, what is the largest angle, in degrees relative to the incident direction, that a boat in the harbor would be protected from the wave action

Answer 1

The angle that the wave would be
`\theta = sin ^(-1)(2 \lambda)/(D)`

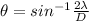
Step-by-step explanation:

From the question we are told that the opening to the harbor acts just like a single-slit so a boat in the harbor that at angle equal to the second diffraction minimum would be safe and the on at angle greater than the diffraction first minimum would be slightly affected

The minimum is as a result of destructive interference

And for single-slit this is mathematically represented as

`D sin \ \theta =m \lambda`

where D is the slit with

`\theta` is the angle relative to the original direction of the wave

m is the order of the minimum j

`\lambda` is the wavelength

Now since in the question we are told to obtain the largest angle at which the boat would be safe

And the both is safe at the angle equal to the second minimum then

The the angle is evaluated as

`\theta = sin ^(-1)[(m\lambda)/(D) ]`

Since for second minimum m= 2

The equation becomes

`\theta = (2 \lambda)/(D)`