Answer:
The fossil is 1860 years old.
Explanation:
The equation for the amount of fossil has the following format:
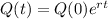
In which Q(t) is the amount after t years, Q(0) is the initial amount and r is the rate of change.
Half-life of c-14 is 5730 years.
This means that

So
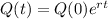
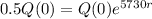
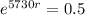
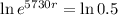
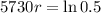
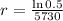
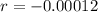
So
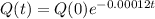
How old is the fossil?
This is t for which
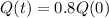
So
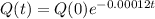

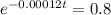
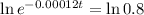
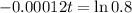

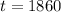
The fossil is 1860 years old.