Answer:
Packaging with cube will be more efficient.
Explanation:
Given:
A cube and a sphere where the diameter of the sphere is equal to the height of the cube.
Let the height of the cube "x"
Radius of the sphere =
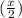
Formula to be used:
Surface area of the cube =
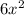 and Surface area of the sphere =
and Surface area of the sphere =
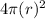
Volume of the cube =
 and Volume of the sphere =
and Volume of the sphere =
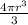
We have to compare the ratio of SA and Volumes.
Ratio of SA : Ratio of their volumes :
⇒
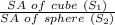 ⇒
⇒
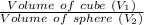
⇒
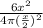 ⇒
⇒

⇒
 ⇒
⇒
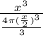
⇒
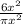 ⇒
⇒

⇒
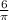 ⇒
⇒
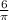
⇒ approx
 ⇒ approx
⇒ approx

⇒
 ⇒
⇒
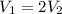
Packaging of the toy with the cube will be more efficient as it has more volume comparatively.