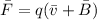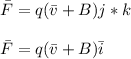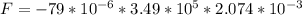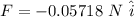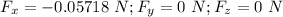Answer:
a)
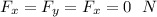
b)
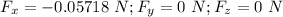
Step-by-step explanation:
Given that:
q = -79 μC
q = - 79×10⁻⁶ C
d = 1.53 cm
d = 0.0153 m
I = 34 A
v = 3.49×10⁵ m/s
The force on charge q is given by
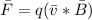
a) At midway (A) , the B will be :
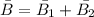
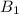 and
and
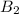 will be equally the same in respect to their magnitude but opposite direction at point A.
will be equally the same in respect to their magnitude but opposite direction at point A.
So;
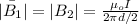
where
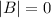
∴
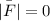
∴
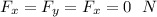
b)
At a distance d/2 cm above the upper wire:
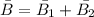
where:
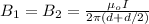 ; upward to the plane of paper
; upward to the plane of paper
∴
![(\mu_o I)/(2 \pi) \ \ [(2)/(3/d) +(2)/(d)] \ \ \hat{k}](https://img.qammunity.org/2021/formulas/physics/college/qdb9rbf0sw39sxu42uv65xi2edruwobf50.png)
B =
![(\mu_o I)/( \pi \ d) \ \ [(1)/(3) +1] \ \ \hat{k}](https://img.qammunity.org/2021/formulas/physics/college/85ryxy87yjeeme1nfimb3a1lb0mfyx79s2.png)
B =
![(\mu_o I)/( \pi \ d) \ [(4)/(3) ] \ \hat{k}](https://img.qammunity.org/2021/formulas/physics/college/lpb3brf0q7n45l6sb24y5zv6dh699cy3kx.png)
B =
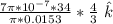
B = 2.074 × 10⁻³T
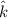
∴