Question

Treatment with statins can reduce the risk of a major cardiovascular event in people with specified risk factors. During about 2 years of follow-up in the JUPITER trial, 142 of 8901 subjects treated with a statin had a major cardiovascular event.

Suppose the expected 2-year risk of a major cardiovascular event in similar but untreated people is 0.028. Test whether the 2-year risk in those treated with a statin is significantly different from this expected risk at the 5% level. Make sure to state your null and alternative hypotheses and specify your conclusion.

Answer 1

We conclude that the 2-year risk in those treated with a statin is significantly different from this expected risk.

Explanation:

We are given that during about 2 years of follow-up in the JUPITER trial, 142 of 8901 subjects treated with a statin had a major cardiovascular event.

Suppose the expected 2-year risk of a major cardiovascular event in similar but untreated people is 0.028.

Let p = proportion of 2-year risk in those treated with a statin

SO, Null Hypothesis,
`H_0` : p = 0.028 {means that the 2-year risk in those treated with a statin is same as of this expected risk}

Alternate Hypothesis,
`H_A` : p
`\\eq` 0.028 {means that the 2-year risk in those treated with a statin is significantly different from this expected risk}

The test statistics that will be used here is One-sample z proportion statistics;

T.S. =
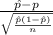`\frac{\hat p-p}{{\sqrt{(\hat p(1-\hat p))/(n) } } } }` ~ N(0,1)

where,
`\hat p` = sample proportion of subjects treated with a statin had a major cardiovascular event =
`(142)/(8901)` = 0.016

n = sample of subjects = 8901

So, test statistics =
`\frac{0.016-0.028}{{\sqrt{(0.016(1-0.016))/(8901) } } } }`

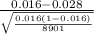
= -9.023

Now at 5% significance level, the z table gives critical values between -1.96 and 1.96 for two-tailed test. Since our test statistics is way higher than the critical values of z as it doesn't lie within the range of critical values of z, so we have sufficient evidence to reject our null hypothesis as it will fall in the rejection region.

Therefore, we conclude that the 2-year risk in those treated with a statin is significantly different from this expected risk.