Answer:
C. The x-coordinate of the vertex must be 6
Explanation:
The parabola intercepts the x-axis when y = 0.
Therefore, if the quadratic equation has the points (2, 0) and (10, 0) then the x-intercepts or "zeros" are x = 2 and x = 10.
The x-coordinate of the vertex is the midpoint of the zeros.
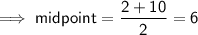
Therefore, the solution is option C.
Additional Information
The leading coefficient of a quadratic tells us if the parabola opens upwards or downwards:
- Positive leading coefficient = parabola opens upwards
- Negative leading coefficient = parabola opens downwards
We have not been given this information and so therefore cannot determine the way in which it opens.
As we do not know the way in which way the parabola opens, we cannot determine if the parabola will have a negative or positive y-intercept.
We have not been given the full quadratic equation, and so we cannot determine if the parabola is wider (or narrower) than the parent function.