Question

9.2.8.

The number of students enrolled at a college is 18,000 and grows 4% each year. Complete parts (a) through (e).


after 22 year there will be how many students

Answer 1

Using the exponential growth formula, after 22 years the college will have approximately 42,066 students enrolled, assuming a 4% annual growth rate.

Step-by-step explanation:

To calculate the number of students after 22 years with an annual growth rate of 4%, we use the formula for exponential growth:

`N = N0 * (1 + r)^t`

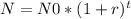
Where:

• N is the future value we want to find,
• N0 is the initial value (18,000 students),
• r is the growth rate (4% or 0.04), and
• t is the time in years (22 years).

Substituting our values into the formula:

`N = 18,000 * (1 + 0.04)^(22)`

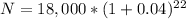
Calculating the compound growth, we have:
N = 18,000 * (1.04)^22

N = 18,000 * 2.336969293
N ≈ 42,065.65

Therefore, after 22 years, the college will have approximately 42,066 students enrolled.

Answer 2

We have been given that the number of students enrolled at a college is 18,000 and grows 4% each year. We are asked to find number of students after 22 years.

We will use exponential growth function to solve our given problem.

We know that an exponential growth function is in form
`y=a\cdot (1+r)^x`, where

y = Final value,

a = Initial value,

r = Growth rate in decimal form,

x = Time

`4\%=(4)/(100)=0.04`

`y=18,000\cdot (1+0.04)^x`

`y=18,000\cdot (1.04)^x`

To find number of students after 22 years, we will substitute
`x=22` in our function.

`y=18,000\cdot (1.04)^(22)`

`y=18,000\cdot (2.3699187915049464)`

`y=42,658.53824`

`y\approx 42,659`

Therefore, there will be approximately 42,659 students after 22 years.