Answer:
0.087 m
Step-by-step explanation:
Length of the rod, L = 1.5 m
Let the mass of the rod is m and d is the distance between the pivot point and the centre of mass.
time period, T = 3 s
the formula for the time period of the pendulum is given by
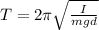 .... (1)
.... (1)
where, I is the moment of inertia of the rod about the pivot point and g is the acceleration due to gravity.
Moment of inertia of the rod about the centre of mass, Ic = mL²/12
By using the parallel axis theorem, the moment of inertia of the rod about the pivot is
I = Ic + md²
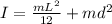
Substituting the values in equation (1)
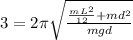
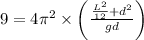
12d² -26.84 d + 2.25 = 0
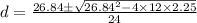
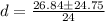
d = 2.15 m , 0.087 m
d cannot be more than L/2, so the value of d is 0.087 m.
Thus, the distance between the pivot and the centre of mass of the rod is 0.087 m.