Answer:
Probability that the 50 randomly selected laptops will have a mean replacement time of 3.1 years or less is 0.0092.
Yes. The probability of this data is unlikely to have occurred by chance alone.
Explanation:
We are given that the replacement times for the model laptop of concern are normally distributed with a mean of 3.3 years and a standard deviation of 0.6 years.
He then randomly selects records on 50 laptops sold in the past and finds that the mean replacement time is 3.1 years.
Let M = sample mean replacement time
The z-score probability distribution for sample mean is given by;
Z =
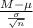 ~ N(0,1)
~ N(0,1)
where,
 = population mean replacement time = 3.3 years
= population mean replacement time = 3.3 years
 = standard deviation = 0.6 years
= standard deviation = 0.6 years
n = sample of laptops = 50
The Z-score measures how many standard deviations the measure is away from the mean. After finding the Z-score, we look at the z-score table and find the p-value (area) associated with this z-score. This p-value is the probability that the value of the measure is smaller than X, that is, the percentile of X.
Now, Probability that the 50 randomly selected laptops will have a mean replacement time of 3.1 years or less is given by = P(M
 3.1 years)
3.1 years)
P(M
 3.1 years) = P(
3.1 years) = P(
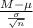

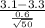 ) = P(Z
) = P(Z
 -2.357) = 1 - P(Z
-2.357) = 1 - P(Z
 2.357)
2.357)
= 1 - 0.99078 = 0.0092 or 0.92%
So, in the z table the P(Z
 x) or P(Z < x) is given. So, the above probability is calculated by looking at the value of x = 2.357 in the z table which will lie between x = 2.35 and x = 2.36 which has an area of 0.99078.
x) or P(Z < x) is given. So, the above probability is calculated by looking at the value of x = 2.357 in the z table which will lie between x = 2.35 and x = 2.36 which has an area of 0.99078.
Hence, the required probability is 0.0092 or 0.92%.
Now, based on the result above; Yes, the computer store has been given laptops of lower than average quality because the probability of this data is unlikely to have occurred by chance alone as the probability of happening the given event is very low as 0.92%.