Question

The Global Positioning System (GPS) is a constellation of about 24 artificial satellites. The GPS satellites are uniformly distributed in a total of six orbits such that there are four satellites per orbit. The number of satellites and spatial distribution insures that at least eight satellites can be simultaneously seen at any time from almost anywhere on Earth.

The GPS satellites circle the Earth at an altitude of about 20,000 km (13,000 miles) and complete two full orbits every day. The GPS satellites are not in a geostationary orbit, but rise and set two times per day. Each satellite broadcast radio waves towards Earth that contain information regarding its position and time. We can receive this information by using special receivers, called GPS receivers, which can detect and decode this information.

By combining signals transmitted by several satellites and received simultaneously, a GPS receiver can calculate its position on the Earth (i.e, its latitude and longitude) with an accuracy of approximately 10m. There are more sophisticated receivers that can be used to determine position with an accuracy of a few millimeters.

G = 6.673 times 10^-11 N m^2/kg^2 R_Earth = 7371 km M_Earth 5.972 kg

Please answer parts A through E.

Confirm that gEarth is about 9.8 m/s^2. (Show work)

Mars has a mass of 6.4 1 7 x 10^23kg and a radius of 2,106 miles. Calculate gMars:

Calculate Earth's gravitational force on a GPS satellite (use orbital radius and not the altitude for distance).

What is the force of gravity on a GPS satellite on Earth (do you even need to calculate it?)

Confirm that a GPS satellite orbiting at an altitude of about 20,000 km does indeed have a period of about 12 hours.

Answer 1

b) 3.72m/s²

c) 9.33*10^5

d) 9.33*10^5

e) 11.85 hrs

Step-by-step explanation:

a) to confirm that gEarth is about 98 m/s².

Let's use the formula:

`gEarth= (G*M)/(R^2)`

`= (6.67*10^-^1^1*5.972*10^2^4)/((6378*10^3)^2)`

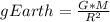
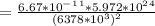
= 9.78 m/s²

=> 9.8m/s²

b) Given:

`m = 6.417*10^2^3`

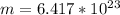
r = 2106 miles

`g_Mars = (G*M)/(R^2)`

`= (6.67*10^-^1^1*6.417*10^2^3)/((2106*1.61*10^3)^2)`

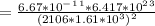
=3.72 m/s²

c) we use:

`F = (G*M*m)/(R^2)`

`=(6.67*10^-^1^1*5.972*10^2^4*1630*10^3)/(((20000+6378)*10^3)^2)`

`= 9.33*10^5 N`

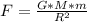
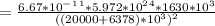
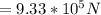
d) Let's take the force of gravitybon earth due to satellite as our answer in (c) because the Earth's gravitational force on a GPS satellite and the force of gravity on a GPS satellite on earth are equal and opposite (two mutual forces).

`F = 9.33*10^5 N`

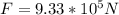
e) In a circular motion,

Gravitional force = Centripetal force.

`(GM*m)/(R^2)=(m*v^2)/(R)`

`(GM)/(R)= v^2`

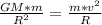
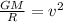
Solving for v, we have

`v= \sqrt{(6*67*10^-^1^1*5.972*10^2^4)/((20000+6278)*10^3)}`

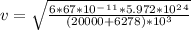
v = 3886m/s

Therefore,

v = 2πR/T

`3886 = (2*pi*(20000+6378)*10^3)/(T)`

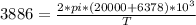
Solving for T, we have:

T = 42650seconds

Convert T to hours

T = 42650/60*60

T = 11.86hrs