Question

Weight gain during pregnancy. In 2004, the state of North Carolina released to the public a large data set containing information on births recorded in this state. This data set has been of interest to medical researchers who are studying the relationship between habits and practices of expectant mothers and the birth of their children. The following histograms show the distributions of weight gain during pregnancy by 840 younger moms (less than 35 years old) and 132 mature moms (35 years old and over) who have been randomly sampled from this large data set. The average weight gain of younger moms is 30.7 pounds, with a standard deviation of 14.91 pounds, and the average weight gain of mature moms is 29.15 pounds, with a standard deviation of 13.46 pounds. Do these data provide strong evidence that there is a significant difference between the two population means? Conduct a hypothesis test. Round all numeric answers to 4 decimal places.1. Which set of hypotheses should the researcher use?

A. H0H0: p1−p2=0p1−p2=0, HAHA: p1−p2<0p1−p2<0
B. H0H0: μ1−μ2=0μ1−μ2=0, HAHA: μ1−μ2≠0μ1−μ2≠0
C. H0H0: p1−p2=0p1−p2=0, HAHA: p1−p2≠0p1−p2≠0
D. H0H0: μ1−μ2=0μ1−μ2=0, HAHA: μ1−μ2>0μ1−μ2>0

2. Calculate the test statistic. ? z t X^2 F =

3. Calculate the p-value for this hypothesis test.
p value =

4. What is your conclusion using αα = 0.01?
A. Do not reject H0H0
B. Reject H0H0

Answer 1

1. B. H0: μ1−μ2=0, HA: μ1−μ2≠0

2. z=1.2114

3. P-value=0.2257

4. Do not reject H0

Explanation:

We have to perfomr an hypothesis test to see if there is strong evidence that there is a significant difference between the two population means.

The null and alternative hypothesis are:

`H_0: \mu_1-\mu_2=0\\\\H_a: \mu_1-\mu_2\\eq0`

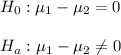
Being μ1 the mean average gain for younger mothers and μ2 the mean average gain for mature mothers.

(NOTE: we are comparing means, not proportions, as it is the random variable is the weight gain).

As we are claiming "strong evidence", the level of significance will be 0.01.

For younger mothers, the sample size is n1=840, the sample mean is 30.7 and the sample standard deviation is s1=14.91.

For mature mothers, the sample size is n2=132, the sample mean is 29.15 and the sample standard deviation is s2=13.46.

The difference between means is

`M_d=\mu_1-\mu_2=30.7-29.15=1.55`

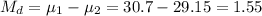
The standard error of the difference between means is

`s_M=\sqrt{(s_1^2)/(n_1)+(s_2^2)/(n_2)}=\sqrt{(14.91^2)/(840)+(13.46^2)/(132)}=√( 0.2647+1.3725)=√(1.6372)\\\\\\s_M=1.2795`

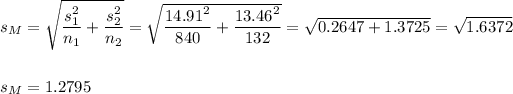
Then, the statistic can be calculated as:

`z=(M_d-(\mu_1-\mu_2))/(s_M)=(1.55-0)/(1.2795)=1.2114`

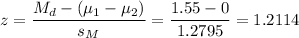
The P-value for this z-statistic in a two tailed test is:

`P-value=2P(z>1.2114)=0.2257`

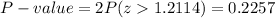
As the P-value is greater than the significance level, the null hypothesis failed to be rejected.

There is no enough evidence to claim that the real average weight gain differs from mature and youger mothers.