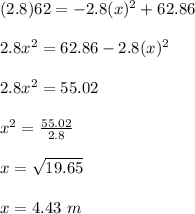Question

The only force acting on a 2.5 kg body as it moves along the positive x axis has an x component Fx = -7x N, where x is in meters. The velocity of the body at x = 2.6 m is 8.5 m/s.

(a) What is the velocity of the body at x = 3.3 m?
(b) At what positive value of x will the body have a velocity of 2.8 m/s?

Answer 1

v = 5.69 m/s

x = 4.43 m

Step-by-step explanation:

Mass of the body m = 2.5 kg

force acting on the body
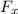`F_x` = - 7 x N

From the Newton's second Law;

`F_x = ma`; Then:

`ma = - 7x\\\\a = (-7x)/(m)\\\\a = (-7x )/(2.5)\\\\a = - 2.8 x\\\\(dv)/(dt) = -2.8x\\\\(dv)/(dx)*(dx)/(dt) = -2.8x\\\\(dv)/(dx)v=-2.8 x\\\\vdv = -2.8dx`

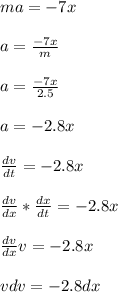
Integrating on both sides ; we have :

`\int\limits {v} \, dv = - 2.8 \int\limits dx \\\\(v^2)/(2)= -2.8(x^2)/(2)+k\\\\`

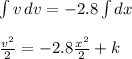
where; k is the integral constant ;

At x = 2.6 m speed is 8.5 m/s

Then;

`(8.5^2)/(2.6)= -2.8(2.6)/(2)+ k\\\\(72.25)/(2.6)= -(7.28)/(2)+k\\\\27.79 = -3.64+k\\\\27.79+3.64 = k\\\\k = 31.43`

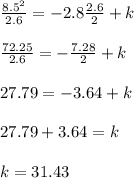
However:

`(v^2)/(2)= (-2.8x^2)/(2)+31.43\\\\\\v^2 = -2.8x^2+62.86 ---- Equation \ 1`

a)

At x = 3.3 m; speed of the object

`v^2 = -2.8 (3.3)^2 +62.86\\\\v^2 = 32.368\\\\v = √(32.368)\\\\v = 5.69 \ m/s`

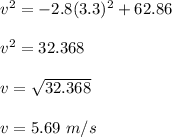
b)

speed of the body is 2.8 m/s; then

`(2.8)62 = -2.8(x)^2 +62.86\\\\2.8x^2 = 62.86 -2.8(x)^2\\\\2.8x^2 = 55.02\\\\x^2 = (55.02)/(2.8)\\\\x = √(19.65)\\\\x = 4.43 \ m`