Question

A 30.0-g object connected to a spring with a force constant of 40.0 N/m oscillates with an amplitude of 6.00 cm on a frictionless, horizontal surface. (a) Find the total energy of the system. 72 mJ (b) Find the speed of the object when its position is 1.15 cm. (Let 0 cm be the position of equilibrium.) m/s (c) Find the kinetic energy when its position is 3.00 cm. mJ (d) Find the potential energy when its position is 3.00 cm. mJ

Answer 1

a) 72mJ

b) 0.33m/s

c) 54mJ

d) 18mJ

Step-by-step explanation:

(a) The total energy of the system is given by:

`E_T=(1)/(2)kA^2`

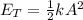
where k is the force constant and A is the amplitude. By replacing we get:

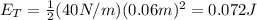`E_T=(1)/(2)(40N/m)(0.06m)^2=0.072J` = 72mJ

(b) we can get the speed by the conservation of energy (the kinetic energy and potential energy must equal the total energy in any place):

`E_T=E_k+E_p\\\\(1)/(2)kA^2=(1)/(2)mv^2+(1)/(2)kx^2\\\\v=\sqrt{(kA^2-kx^2)/(m)}=\sqrt{((40N/m)((0.06m)^2-(0.0115m)^2))/(0.03kg)}=0.33m/s`

where we have used that x=1.15cm=0.0115m; A=6.00cm=0.06m

(c) Again, by the conservation of energy:

`E_k=(1)/(2)k(A^2-x^2)=(1)/(2)(40N/m)((0.06m)^2-(0.03m)^2)=0.054J=54mJ`

(d)
`E_p=(1)/(2)kx^2=(1)/(2)(40.0N/m)(0.03m)^2=0.018J=18mJ`

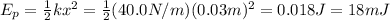
hope this helps!!