Answer:
(a) 2.4s
(b) 0.41Hz
(c) 26.5cm
(d) 68.1m/s
Step-by-step explanation:
(a) To calculate the period we can use the formula:
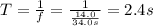
(b) the frequency is the inverse of period:
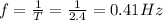
(c) The amplitude is the max distance to the equilibrium position, that is:
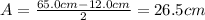
(d) the maximum speed of the glider can be computed by using:

hope this helps!!