Question

Show that a body projected vertically up from the ground, the distance travelled by it in the last second of its upwards motion is an constant independent of its initial velocity

Answer 1

Answer and explanation:

Let
`v_1` be the velocity of a body projected vertically up, 1 second before it reaches its maximum height. We know, from the kinematics equations, that the distance traveled
`y` in an interval of time
`t` is equal to:

`y=v_0t-(1)/(2)gt^(2)`

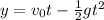
Then, in the last second, the distance traveled
`y_1` is equal to:

`y_1=v_1t-(1)/(2)gt^(2)`

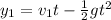
But the velocity
`v_1` is related to the time by the equation:

`t=(v_1)/(g)\\\\v_1=gt`

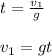
And substituting this expression in the equation above, we obtain:

`y_1=gt^(2)-(1)/(2)gt^(2)\\\\y_1=(1)/(2)gt^(2)\\\\y_1=(1)/(2)(9.8m/s^(2))(1s)^(2)\\ \\y_1=4.9m`

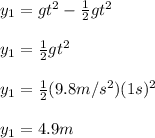
It means that the distance traveled by the body in the last second of its motion is a constant, independent of its initial velocity.