Question

A doubly drained specimen, 2.54 cm in height, is consolidated in the lab under an applied stress. The time for 50 % overall (or average) consolidation is 12 min. (a) Compute the cv value for the lab specimen. (b) How long will it take for the specimen to consolidate to an average consolidation of 90 %? (c) If the final consolidation settlement of the specimen is expected to be 0.43 cm, how long will it take for 0.18 cm of settlement to occur? (d) After 14 minutes, what percent consolidation has occurred at the middle of the specimen?

Answer 1

Cv = 0.026 cm²/min

t = 52.60 min

v% = 41.86 %

tv = 0.1375

t = 8.53 min

v = 53.61 %

Step-by-step explanation:

given data

height = 2.54 cm

50 % consolidation = 12 min

solution

we get here first Cv value that is express as

Tv =
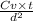`(Cv* t)/(d^2)` .................1

here Tv for 50% is 0.196

put here value and we get

0.196 =
`(Cv* 12)/((2.54)/(2)^2)`

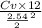
solve it we get

Cv = 0.026 cm²/min

and

for tv for 90 % consolidation is 0.848

put value in equation 1

0.848 =
`(0.026* t)/((2.54)/(2)^2)`

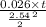
solve it we get t

t = 52.60 min

and

v% will be here is

v% =
`(0.18)/(0.43) * 100`

v% = 41.86 %

and

tv =
`(\pi )/(4)* (4)/(100)^2`

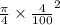
tv = 0.1375

so now put value in equation 1 we get

0.1375 =
`(0.026 * t)/((2.54)/(2)^2)`

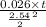
solve it we get

t = 8.53 min

and

now put value of t 14 min in equation 1 will be

tv =
`(0.026 * 14)/((2.54)/(2)^2)`

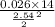
t = 0.225 min

and v will be after 14 min

0.0225 =
`(\pi )/(4)* (v)/(100)^2`

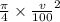
v = 53.61 %