Question

Suppose we are interested in analyzing the weights of NFL players. We know that on average, NFL players weigh 247 pounds with a population standard deviation of 47 pounds. Suppose we take a sample of 30 new players and we find that the average weight from that sample is 237 pounds. We are interested in seeing if the weight of NFL players is decreasing

a.What is the standard error?

b.What is the margin of error at 90% confidence?

c. Using my sample of 30, what would be the 90% confidence interval for the population mean?

Answer 1

a) The standard error would be of 8.58 pounds.

b) The margin of error is 14.11 pounds.

c) The 90% confidence interval for the population mean is between 232.89 pounds and 261.11 pounds

Explanation:

Answer 2

a) The standard error would be of 8.58 pounds.

b) The margin of error is 14.11 pounds.

c) The 90% confidence interval for the population mean is between 232.89 pounds and 261.11 pounds

Explanation:

a.What is the standard error?

The standard error is

`s = (\sigma)/(√(n))`

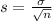
In which
`\sigma` is the standard deviation of the population and n is the size of the sample. So

`s = (47)/(√(30)) = 8.58`

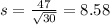
The standard error would be of 8.58 pounds.

b.What is the margin of error at 90% confidence?

We have that to find our
`\alpha` level, that is the subtraction of 1 by the confidence interval divided by 2. So:

`\alpha = (1-0.9)/(2) = 0.05`

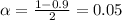
Now, we have to find z in the Ztable as such z has a pvalue of
`1-\alpha`.

So it is z with a pvalue of
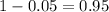`1-0.05 = 0.95`, so
`z = 1.645`

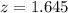
Now, find the margin of error M as such

`M = z*s = 1.645*8.58 = 14.11`

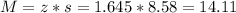
The margin of error is 14.11 pounds.

c. Using my sample of 30, what would be the 90% confidence interval for the population mean?

Lower bound: Sample mean subtracted by the margin of error.

247 - 14.11 = 232.89 pounds

Upper bound

247 + 14.11 = 261.11 pounds

The 90% confidence interval for the population mean is between 232.89 pounds and 261.11 pounds