Question

Hurrrryyyyy plllzzz. Determine the equation of the line that passes through the given points

(10,2) and (-3,2)

Answer 1

y = 2

Explanation:

To determine the equation of the line that passes through (10,2) and (-3,2), we need to determine the slope of the line. Then substitute the slope and any given point in point slope form to obtain the equation of the line.

Finding the Slope of the line:

`\implies \text{Slope} = \frac{\text{Rise}}{\text{Run}} = (y_(2) - y_(1) )/(x_(2) - x_(1) )`

`\implies \text{Slope} = (y_(2) - y_(1) )/(x_(2) - x_(1) )`

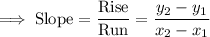
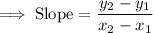
Substitute the coordinates of the given points:

`\implies \text{Slope} = (2 - 2)/(-3 - 10 )`

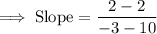
Simplify the equation to determine the slope:

`\implies \text{Slope} = (0)/(-3 - 10 )`

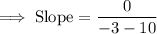
∴ 0 divided by ANY number is ALWAYS 0.

`\implies \text{Slope} =0`

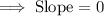
Finding the equation of the line:

Point slope form formula: y - y₁ = m(x - x₁)

• x₁ and y₁ are the coordinates of any given point.
• m is the slope

Substitute the values in the point slope form:

`\implies \text{Equation of line:} \ y - y_(1) = m(x - x_(1) )`

`\implies \text{Equation of line:} \ y - 2 = 0(x - 10)`

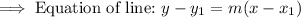
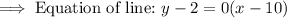
Simplify the equation to determine the equation of the line:

∴ Any number multiplied by 0 is 0.

`\implies \text{Equation of line:} \ y - 2 = 0`

`\implies \text{Equation of line:} \ y = 0 + 2`

`\implies \text{Equation of line:} \ y = 2`

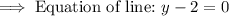
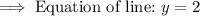
Thus, the equation of the line is y = 2.