Question

Suppose that a biker bikes into the wind for 84 miles and it takes him 7 hours. After a long rest, he returns (with the wind on his back) in 6 hrs. Determine the speed at which biker can ride his bike in still air and the effect that the wind had on his speed.

Answer 1

Speed of the biker is 13 mph and that of wind is 1 mph.

Explanation:

Given:

Time taken by the biker to cover a distance is 7 hrs when he was travelling against the speed of the wind.

Time taken to cover same distance is 6 hours when he was travelling with the speed of the wind.

We have to find the speed of the biker and that of the wind.

Let the speed of the biker is "b" mph

And the speed of the wind is "w" mph

As we know:

Distance = Product of speed and time

Re-arranging the above situation in terms of equation.

⇒
`(b-w)* 7 = 84` ⇒
`(b+w)* 6 =84`

⇒
`7b-7w=84` ...(i) ⇒
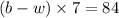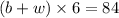
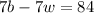`6b+6w=84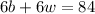`...(ii)

Multiplying equation (i) with 6 and equation (ii) with 7 so that we can eliminate one variable that is "w" after adding both the equation.

⇒
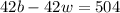`42b-42w=504` equation (iii)

⇒
`42b+42w=588` equation (iv)

⇒ Adding both the equations.

⇒
`84b=1092`

⇒
`b=(1092)/(84)`

⇒
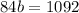
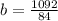
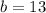`b=13` mph.

Speed of the biker is 13 mph.

⇒ Plugging b=13 in equation (ii),we have:

⇒
`6b+6w=84`

⇒
`6w=84-6b`

⇒
`6w=84-6(13)`

⇒
`6w=84-78`

⇒
`6w=6`

⇒
`w=(6)/(6)`

⇒
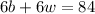
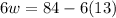
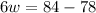
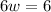
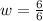
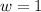`w=1` mph.

Speed of the biker is 13 mph and the speed of the wind is 1 mph whenever the biker is with the speed of the wind the biker's speed increases by 1 mph and subsequently decreases when he is against the speed of the wind.