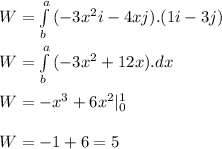Question

Find the work done by the force bold upper f equals xy bold i plus left parenthesis y minus x right parenthesis bold jf=xyi+(y−x)j over the straight line from left parenthesis 0 comma 0 right parenthesis(0,0) to left parenthesis 1 comma negative 3 right parenthesis(1,−3).

Answer 1

Workdone = 5 units

Explanation:

Given:-

- The force is defined in cartesian coordinates:

F = xy i + (y-x) j

- Acts for the line between two points:

( 0 , 0 ) & ( 1 , -3 )

Find:-

Find the work done by the force over the straight line.

Solution:-

- The work-done by an force is defined as a dot product of Force (F) and the path at which the force acts (ds) or a path integral of force.

`W = \int\limits^a_b {F} . ds`

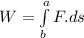
- The path (ds) is defined as straight line between two points. We will determine the equation of line:

y = mx + c

Where, m = ( -3 - 0 ) / ( 1 - 0 ) = -3

c = 0

y = -3x

- We will substitute the value above into Force F:

F = x(-3x) i + (-3x-x) j

F = -3x^2 i - 4x j

- Now evaluate the integral for Work done:

`W = \int\limits^a_b {(-3x^2i - 4xj}) . (1 i -3j)\\\\W = \int\limits^a_b {(-3x^2 + 12x}).dx\\\\W = -x^3 + 6x^2 |^1_0\\\\W = -1 + 6 = 5`