Question

A person places $419 in an investment account earning an annual rate of 9.2%, compounded continuously. Using the formula V=PertV=Pe rt, where V is the value of the account in t years, P is the principal initially invested, e is the base of a natural logarithm, and r is the rate of interest, determine the amount of money, to the nearest cent, in the account after 20 years.

Answer 1

`V=\$2638.25`

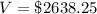
Explanation:

From the given information

Principal Initially Invested, P =$419

Annual Rate, r=9.2% =0,092

Time, t = 20 Years

Since it is compounded continuously, the value after t years is determined using the given model:

`V=Pe^(rt)`

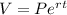
Substituting the given values

`V=419*e^(0.092*20)\\V=\$2638.25`

The value of the account after 20 years is
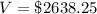`V=\$2638.25` (correct to the nearest cent)