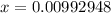Answer:
The distance the mass would stretch it is
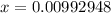
The correct option is A
Step-by-step explanation:
From the question we are told that
The period of the slit is
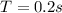
The acceleration due to gravity is
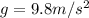
Generally the period is mathematically represented as
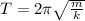
Whee m is the particle and k is the spring constant
making
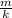 the subject
the subject
![(m)/(k) = [(T)/(2 \pi) ]^2](https://img.qammunity.org/2021/formulas/physics/college/yuqen3s5t5gjcermh0q7qbiiafgzbjmpmr.png)
The weight on the particle is related to the force stretching the spring by this mathematical relation
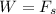
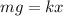
where x is the length by which the spring is stretched
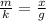
Substituting the equation above for
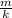
![[(T)/(2 \pi) ]^2 = (x)/(g)](https://img.qammunity.org/2021/formulas/physics/college/88dcwmkkafx4mb47x129lc1ydry322g48j.png)
making x the subject
![x = g [(T)/(2 \pi) ]](https://img.qammunity.org/2021/formulas/physics/college/nknso4p5xuwk4bq7jt6nlli16nk0x10r7q.png)
Substituting the value
![x = 9.8 * [(0.2)/(2 * 3.142) ]^2](https://img.qammunity.org/2021/formulas/physics/college/xgvfmb378t8huk2xugeatev022aiy608qo.png)