Question

Assume that the profit generated by a product is given by where x is the number of units sold. If the profit keeps changing at a rate of per month, then how fast are the sales changing when the number of units sold is 1100? (Round your answer to the nearest dollar per month.) $30/month $132,665/month $16,583/month $33,166/month

Answer 1

P'(1100)=0.06

(see explanation below)

Explanation:

The answer is incomplete. The profit function is missing, but another function will be used as an example (the answer will not match with the options).

The profit generated by a product is given by
`P=4√(x)`.

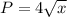The changing rate of sales can be mathematically expressed as the derivative of the profit function.

Then, we have to calculate the derivative in function of x:

`(dP)/(dx)=(d[4x^(0.5)])/(dx)=4(0.5)x^(0.5-1)=2x^(-0.5)=(2)/(√(x))`

We now have to evaluate this function for x=1100 to know the rate of change of the sales at this vlaue of x.

`P'(1100)=(2)/(√(1100) ) =(2)/(33.16) =0.06`