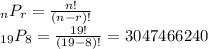Answer:
1. 75582
2. 3047466240
Explanation:
1. If order does not matter, this is a combination problem. You are choosing 8 sticks from a set of 19. (Octagons have 8 sides.)
The formula for combinations of n things chosen r at a time "n choose r" is
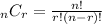
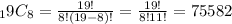
2. If order matters, there are more possibilities. This is a permutation problem. The number of permutations of 19 things taken 8 at a time, "19 permute 8" is