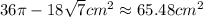Question

A right triangle is inscribed in a circle as shown. What is the area of the shaded region. Diameter of 12 and 9 cm in triangle

Answer 1

`36\pi -18√(7)`

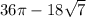
Explanation:

Every inscribed right triangle has its hypotenuse as the same size of the Diameter. Assuming that, this is the case check the picture below.

So the hypotenuse= D=2R=12

1. Shaded Area = Area of the Circle- Area of the Triangle

• Area of Circle:

`A_(circle)=\pi (6)^(2)=36\pi`

• Area of the Triangle:

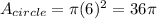
Finding the Triangle base via the Pythagorean Theorem

`a^2=b^2+c^2\\12^2=9^2+c^2\\144-81=c^2\\c=√(63)\\c=3√(7)\approx 7.94`

Now plugging in the base of the triangle on that formula:

`A=(bh)/(2)\\A=(3√(7)*12)/(2)\\A=18√(7)`

Finally,

Shaded Area =
`36\pi -18√(7) cm^(2) \approx 65.48 cm^(2)`