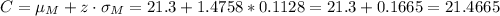Question

A particular variety of watermelon weighs on average 21.3 pounds with a standard deviation of 1.07 pounds. Consider the sample mean weight of 90 watermelons of this variety. Assume the individual watermelon weights are independent. a. What is the expected value of the sample mean weight

Answer 1

The expected value of the sample mean weight of watermelons, given a population mean of 21.3 pounds, is also 21.3 pounds.

Step-by-step explanation:

Expected Value of the Sample Mean Weight of Watermelons

If we have a population in which the average watermelon weighs 21.3 pounds with a standard deviation of 1.07 pounds, and we consider the sample mean weight of 90 watermelons, we can calculate the expected value of this sample mean. In statistics, the expected value of the sample mean is the same as the population mean when the samples are drawn from the population independently. Thus, the expected value of the sample mean weight for the watermelons is 21.3 pounds.

Answer 2

a) expected value = 21.3 pounds

b) standard deiation of the sample mean weight = 0.1128

c) P(x>21.3)=0.5000

d) C=21.4665

Step-by-step explanation:

The question is incomplete:

b. What is the standard deviation of the sample mean weight? Give your answer to four decimal places. 2

c. What is the approximate probability the sample mean weight will be greater than 21.3? Give your answer to four decimal places. Use the standard deviation as you entered it above to answer this question. 3

d. What is the value c such that the approximate probability the sample mean will be less than c is 0.93? Give your answer to four decimal places. Use the standard deviation as you entered it above to answer this question. 4

We have the parameters of the population of melon weights (mean: 21.3 pounds, standard deviation: 1.07 pounds) and we have to describe the sampling distribution of sample means, when the sample size is n=90.

The mean of the sampling distribution (the expected value of the sample mean weight) is equal to the population mean: 21.3 pounds.

The standard deviation of the sampling distribution is calculated as:

`\sigma_M=\sigma/√(n)=1.07/√(90)=1.07/9.49=0.1128`

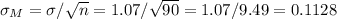
As the mean of the sampling distribution is 21.3, the probability that the sample mean exceeds 21.3 pounds is P=0.5000.

Now, to calculate C so that P(x<c)=0.93 we have to look up for the z-scor z* so that P(z<z*)=0.93.

According to the standard normal distribution, this z-score is z*=1.4758.

Then, we can convert this value to our specific distribution and calculate c as:

`C=\mu_M+z\cdot \sigma_M=21.3+1.4758*0.1128=21.3+0.1665=21.4665`