Answer:
The interval is (2.7512, 2.8488)
Explanation:
Given that:
The mean (μ) = 2.9 hours
The standard deviation (σ) = 0.24 hours
n = 14 pound turkey
The confidence interval (c) = 95% = 0.95
α = 1 - 0.95 = 0.05
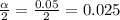
The Z score of
 is the z score of 0.025 which is the same z score of 0.475 (0.5 - 0.025).
is the z score of 0.025 which is the same z score of 0.475 (0.5 - 0.025).
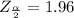
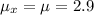
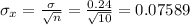
Therefore the margin of error E is given as
E =
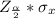 = 1.96 × 0.0759 = 0.1488
= 1.96 × 0.0759 = 0.1488
The interval is
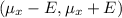 = (2.9 - 0.1488, 2.9 + 0.1488) = (2.7512, 2.8488)
= (2.9 - 0.1488, 2.9 + 0.1488) = (2.7512, 2.8488)
The interval is (2.7512, 2.8488)