Answer:
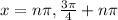
Explanation:
Since we have a product here, either term can be zero. We can individually set each term equal to zero:
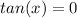
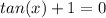
Beginning with the first term. It is saying "tangent of what gives zero". Well, tangent of zero gives zero. The value pi also gives zero:
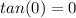

We can generalize this by saying 'x' is equal to pi multiplied by an integer 'n', where 'n' is 0, 1, 2, 3...
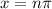
Moving on to the second term, lets subtract that 1 to the other side to get:
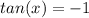
Tangent of what gives -1? That would be 3pi/4. Tangent is the ratio of sine and cosine. So, you can essentially think of tangent as the slope of the line on a unit circle. Refer to the figure below. Another location along the unit circle where we get -1 is at 7pi/4, which is just 3pi/4 shifted by 180 degrees. Therefore, we can generalize this solution by adding 'npi' to 3pi/4 to get:
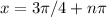
where 'n' is 0, 1, 2, 3...