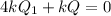Answer:
a)
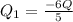
b)

Step-by-step explanation:
Given:
Radius = R
Inner radius = 2R
Outer radius = 3R
a) For charge when sphere is conducting:
Lets take Q1 as the charge on inner sphere, which means a charge of
-Q1 wil be induced on the outer sphere.
Let's find the net potential at center of the sphere,
We now use the expression:
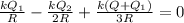
Multiplying through by R, we have:
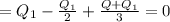
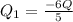
b) for charge when sphere is non-conducting.
Let thee net field inside of the sphere beween R1<r<R2 be considered as zero.
Therefore the inner surface charge induced in the sphere will be -Q as to get net charge close to zero.
For zero net potential at the center, we have: