Question

Pulling out of a dive, the pilot of an airplane guides his plane into a vertical circle. At the bottom of the dive, the speed of the airplane is 320 m/s. What is the smallest radius allowable for the vertical circle if the pilot's apparent weight is not to exceed 7.0 times his true weight

a. 2200 m
b. 230 m
c. 42 m
d. 1700 m
e. 1500 m

Answer 1

The radius allowable for the vertical circle is 1706 meters.

Step-by-step explanation:

Given that,

Speed of the airplane, v = 320 m/s

We need to find the smallest radius allowable for the vertical circle if the pilot's apparent weight is not to exceed 7.0 times his true weight . At the bottom of circle, net force is given by :

`F_N=F_c+F_g\\\\F_N=m((v^2)/(r)+g)\\\\7gm=m(9.8+((320)^2)/(r))`

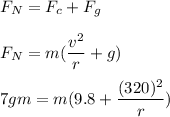
r is radius of path

`7* 10=(10+((320)^2)/(r))\\\\r=1706\ m`

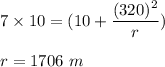
So, the radius allowable for the vertical circle is 1706 meters.