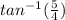z= r(cosθ+i sinθ) is the required polar form where, r = √41 and θ =π-
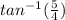
Explanation:
Given,
-4+5i is a complex number.
To find the polar form.
Formula
z=x+iy
r² = mod of (x²+y²)
θ =
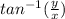
So, the polar form will be z=r(cosθ+i sinθ)
Now,
r² =(-4)²+5² = 41
or, r = √41
θ =π-
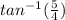 [ since the point is in second quadrant]
[ since the point is in second quadrant]
Hence,
z= r(cosθ+i sinθ) is the required polar form where, r = √41 and θ =π-