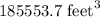Answer:
Explanation:
GIVEN: A space telescope on a mountaintop is housed inside of a cylindrical building with a hemispheric dome. If the circumference of the dome is
 , and the total height of the building up to the top of the dome is
, and the total height of the building up to the top of the dome is
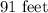 .
.
TO FIND: what is the approximate total volume of the building.
SOLUTION:
let the height of the mountaintop be
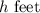
As the dome hemispherical.
circumference of a hemisphere
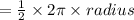
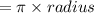
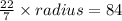
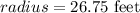
total height of the building up to the top of the dome
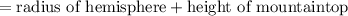
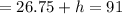
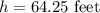
Volume of building
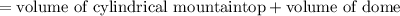
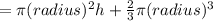
as radius of mountain top is same as dome
putting values
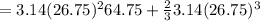
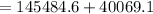
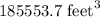
Hence the total volume of the building is