Question

The areas of the squares adjacent to two sides of a right triangle are 29.25 units 2 and 13 units 2 . Find the length,x, of the third side of the triangle

Answer 1

The length of the third side of the triangle = 6.5 units

Explanation:

Here, we have the location of the square given by the adjacent and the opposite sides to the other angles of the right triangle which are < and sum up to 90°

From the given areas of the squares, the length of the two sides of the right angled triangle are √13 and √29.25

The length of the third side is given by

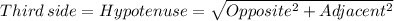
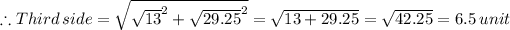`Third \, side = Hypotenuse = √(Opposite^2 + Adjacent^2)`

`\therefore Third \, side = \sqrt{√(13) ^2 + √(29.25)^2 } = √(13 + 29.25) = √(42.25) =6.5 \, unit`.

Answer 2

6.5units

Explanation:

Find the length side of the smaller square

The area of the square is equal to

A = a^2

so

a^2 = 13

a = √13 units

step 2

Find the length side of the larger square

The area of the square is equal to

A = b^2

so

b^2 = 29.25

b = √29.25 units

step 3

Find the value of x

Applying the Pythagoras Theorem

x^2 = a^2 + b^2

x^2 = 13 + 29.25

x^2 = 42.25 units

x = √42.25

x = 6.5 units